The Theory that Would Not Die starts out strong. This history of Bayesian thought by Sharon Bertsch McGrayne was recommended to me after I finished reading a biography of Claude Shannon, and I was pretty excited to read about how Bayesian thought developed before and after Shannon.

The first few chapters were a great introduction to the Reverend Thomas Bayes, to Pierre-Simon Laplace, and to some of the controversies of the early 1800s. Going into this book, I thought that I understood the origin of Bayes’ rule, and just had to learn about how it became popular now. My preconception was exactly backwards.

The myth of Bayes rule is that Bayes himself created it to address a question from David Hume about the existence of god. Hume claimed that our experience of the world says there can’t be miracles. Since we’ve never seen a miracle, if someone reports one we should always believe they’re mistaken (or lying). Bayes supposedly created his formula to prescribe exactly how much hearing about a miracle should increase our belief in god.

It turns out that there’s very little evidence that Bayes was thinking about that when he created his rule. He wrote a single paper about his rule, in the form of a probabilistic thought experiment involving tossing balls onto a table. That paper was published after Bayes died, along with some religious interpretations of it written by Bayes’ friend who found that paper in Bayes’ effects.

At this point, everyone forgets about it. Pierre-Simon Laplace, facing some very complicated data analysis problems in astronomy and biology, re-invents something very similar to Bayes rule a few decades later. It was Laplace, and not Bayes, who really popularized the idea of “the probability of causes” for the first time. He used it extensively for many of the problems that he faced, and only learned about Bayes’ paper by chance. Apparently Bayes’ prior probabilities (always equal odds) were new to Laplace, and Laplace then incorporated that idea into Laplace’s formulation.

After Laplace died, few people used his methods. There seems to have been some form of smear campaign against Laplace, with people actively avoiding methods he’d created. It wasn’t until the world wars that people started using the probability of causes again.

From WWI up to the present day, the military seems to have been a great user of Bayes’ rule. While statisticians and other academics were debating the merits of Bayes’ equal prior and finding it groundless, the militaries of the world were using Bayesian updating in everything from aiming guns to cracking codes. The military used it because it worked, the academics rejected it because they couldn’t see how it could make sense.

There were some notable academics who embraced Bayes’ rule around this time, especially Turing and Shannon. The book gives a pretty good overview of what Turing accomplished. I was left even more impressed with Turing after this, and even more upset at his treatment by Britain after the war. The book unfortunately didn’t really go into detail on Shannon’s use of Bayes’ rule.

During WWII, breaking German and Japanese codes was crucial to the war effort. The British didn’t really understand that cryptography had advanced since the 1800s, and had to be given the solution to early Enigma cyphers. Polish mathematicians had managed to crack it before the war began. Britain then hired Turing to expand on the Poles’ work, and he basically created modern computing in order to do it. A large part of his work was generating likely priors for different messages. Then using Bayesian updating to determine the rest of the message. After the war, all of his work was made confidential and Turing sworn to secrecy. He was later hounded into suicide by the British government.

After this period, a lot of arguing happened. That’s my best summary of the rest of the book. Many of the Post-WWII chapters were just chronicles of the arguments between people I’d never heard of before.

Each chapter was nominally about some use of Bayes’ rule in history. For the period after WWII, these chapters were arranged moderately chronologically so you could see how Bayes’ rule was rejected and embraced in various times and places. That overall structuring makes sense, so it’s unfortunate that the book didn’t work at all.

The book really played up the personalities of the people involved, and ignored the actual math to a large extent. McGrayne avoided in depth discussions of the math. There was maybe a handful of equations in the entire book. For a history of math, that’s pretty unhelpful. I was hoping to understand how the theory was developed, how new pieces that made Bayes’ workable in the modern world actually worked. Instead I got to read pages and pages about how various people were all jerks to each other.

The emphasis on what Bayes’ rule was used on, and the people who used it, also caused the book to feel very chaotic. The chapters were nominally in historical order, but the later chapters especially jumped around a lot in the careers of various people. I ended up reading about someone in one chapter for three pages, forgetting about him for 50 pages, and then seeing him again in another chapter with the assumption that I would still remember why he was important. I went into this book looking for a high level overview of a theory’s development, and instead of got the knitty-gritty back and forth between dozens of people over the course of decades. For me, this level of detail obscured the higher level points I was reading for.

I would have loved to see more discussion of the math. More simplified examples of what the people were actually working on, and how they were trying to do it. More equations in my math book, in other words.

I was also pretty surprised by what the book focused on in later chapters. It discussed Kalman filters only tangentially, in spite of the fact that they are an incredibly useful and common application of Bayes’ rule. I was waiting for the Kalman filter chapter with baited breath, and it never came. Instead I just got one sentence about how Kalman himself claimed that his filter wasn’t Bayesian at all.

This is such a missed opportunity! The book spends pages and pages talking about how hard it was for Bayesians to get recognized, and the little arguments between Bayesians and frequentists. Then it can’t spend a single page talking about the Kalman filter or why Kalman didn’t think it was Bayesian? The Kalman filter led the development of a huge family of Bayesian filters and models that are used in all of aviation today. Instead we get an entire chapter about some rando who got sent to Europe to look for a submarine. That’s cool and all, but what about the entire space program?

The lack of discussion on Kalman filters, throwing mathematical terms around without helping the reader understand them, the lengthy digressions into tiny spats between statisticians. All of this makes me question how the topics the book focused on were chosen. I’m left wondering whether I actually got a useful history of Bayesian thought, or just the tidbits that this author was particularly interested in.

This was disappointing, as the first few chapters were so good. My recommendation: read through to the end of WWII, then find a different book.

A friend on facebook recently asked for examples where people believed something wrong on purpose, just to improve their lives in some way.

While the idea seemed strange to me at first, I’ve slowly come to realize that there’s something similar that I’m doing in my thinking about my kids. And I think that thing is actually very important to raising my kids well.

Unlike the original request for examples, I’m not trying to believe something I know in my heart is untrue. Instead, I’m actively trying to avoid learning certain things about my kids. Or perhaps it would be better to say that I’m actively avoiding trying to build certain models about my kids.

Self-Fulfilling Models

My kids are very young, only two and a half right now. That means that there’s an enormous amount about who they are (or will be) as people that is unknown right now. Will they be interested in arts or sciences (or both)? Will they be introverts or extroverts? Will they like science fiction or mysteries?

Our kids aren’t super messy when they eat. The main exception to that is yogurt. When we feed them yogurt, it gets all over their faces, their arms, their shirts. The yogurt gets everywhere. After they’ve finished eating it, I’ll come in with a cloth to clean them up. Doing this makes it really obvious that they’re using one hand more than the other. One hand is usually pretty clean, and the other is so covered in yogurt it looks like melted wax.

I actively try not to pay attention to which hand it is. I try to avoid putting together patterns about whether the messy hand changes each time they eat yogurt or not. I try to avoid pointing it out to them.

My goal is to let them develop their handedness, left or right, independently of my own preconceptions. I don’t want to push them to use a hand that they’re not interested in using, or to prematurely settle on using only one hand.

Especially now, during this time of covid-induced hibernation, my kids get the majority of their understanding of the world and what’s good from me. How I think about them influences how I treat them, and how I treat them has an outsized impact on how they grow. I don’t want my own peculiarities to unduly shape who they could be as people.

The importance of letting kids be themselves

Whether our kids are left handed or right handed isn’t a huge deal (but it was historically). On the other hand, there are some personal traits that will have a major influence on my children’s lives. I’m trying to avoid learning those or modeling them as well.

The biggest example of this is intelligence. There’s a whole argument about what “intelligence” means for kids, how correlated intelligence in one domain is with another domain, how it changes with age, and how easy it is to determine. I want to sidestep all of that by appealing to a twin study.

Specifically, a study of my twins. They’re fraternal twins, so genetically different but same environment. They look different and they act different. They also figure things out at different rates. One of my kids is much more verbal than the other, much faster in answering questions, and much better at remembering (or at least repeating) song lyrics.

In spite of how I try not to notice that disparity, it still surprised me when the disparity was disrupted. I taught the kids how to play “I spy…” the other day. The kid who is faster at answering questions and filling in song lyrics really struggled with understanding how the game is played or what the point of it was. The other kid, who is generally quieter and slower to answer questions, understood how the game is played immediately and joined in.

I’ve heard some parents talk about their kids as being “smart” or “slow”. I don’t think either of those models are very helpful to actually raising kids. To me, what seems most important is what would challenge a kid at any given moment. Regardless of what a kid is capable of now, the goal is still to raise the most competent, compassionate, and grounded kids that I can.

For me as a parent, it doesn’t matter if one kid is learning something faster than another. What matters is how I can help both of them learn and grow as effectively as possible. That’s going to be different for each kid, but my overall job is the same.

If I get wrapped up in comparing my kids to each other, or to some arbitrary “standard” development track, that makes it harder for me to do my real job of raising them.

On modeling humans

None of this is to say that I don’t think the idea of intelligence is useful (or similar summary measures like “compassionate” or “grounded”, for that matter). I actually do think summarizing a person as being “smart” can really help when you’re trying to figure out whether to hire person A or person B for a job. Or when you’re trying to decide what leader to elect. Or when you’re thinking about who you trust to have good information about something.

If I were a perfectly fair person, this would be less of an issue. If I were actually able to use my models of the world only when they were applicable, and ignore them when they weren’t applicable, then this wouldn’t matter. I could go ahead and think of one of my kids as left-handed, or estimate their intelligence right now, and not let it impact how I raised them.

But I am not perfectly fair. If I start modeling a person, my model of them will influence every thought I have about them. I can’t even avoid modeling them. When I notice someone answering a question quickly, that automatically leads me to thinking certain things about them. When I notice them usually using their left hand, I automatically label them left-handed.

This is why I actively try to avoid making certain observations about my kids. It’s why I actively try to avoid letting certain observations coalesce into models of them. I know my job, and it’s not judging them. It’s nurturing them. As a human myself, that’s easiest to do when I haven’t already decided what they’ll grow into.

PS

Just to be clear, I also think my kids are both very smart. And caring, creative, athletic, and cute. I’m so proud of them for all of that, but those adjectives aren’t useful when figuring out what games to play or what to teach them next.

A while ago I stumbled on the blog Acoup, which is mostly military history written by an Assistant Professor of history at NCSU. As I binged through the blog’s backlog, I stumbled on a series about Sparta that totally surprised me. Here’s a post I made about it on Facebook.

“When I read about real Spartan history recently, I was pretty surprised that they were only mediocre as individual warriors, they were terrible at warfare in general, and were incredibly brutal to their absolutely huge numbers of slaves.”

This started a fascinating argument about Greek history. It seems like everyone pretty much agrees that Sparta was pretty brutal to their lower classes (though I had had no idea about that until I read the blog posts). What people disagree about is whether they were good at war. This makes sense, given that it’s such a staple of popular culture. Some of the people in that FB discussion know way more history than I do, so I ended up unsure how to weight their statements against those of Acoup.

A friend recently posted a fact-check of some of Acoup’s Sparta claims. That gave me more trust in Acoup’s other claims.

In the end, I remain pretty convinced by Acoup’s claims about Sparta’s (lack of ) prowess at naval and siege warfare, as well as logistics. Where I was left most confused was in the claims about hoplite warfare. As one of my friends mentioned in that FB argument:

“[W]e’re talking about putting down a lot of skilled contemporary analysis. The idea that [historical sources like Xenophon] were just suckered and there’s nothing to it is almost shockingly arrogant, given the scope of their capabilities and accomplishments. As far as I can tell essentially no contemporary sources are like ‘actually, the Spartans are bad and unimpressive’.”

The crux of the argument

everybody: Spartans were the best warriors in the world
Acoup: Spartans society was horrible to live in and highly immoral by modern standards. Also they didn’t win very many wars.
Me (on FB): Seems like Spartans were terrible at warfare
FB friends: they were actually great warriors, and everybody in antiquity knew it

It’s easy to get side-tracked by these types of arguments. The overall idea of Spartans in pop culture is definitely that they’re peak warriors. When I argued with people who defend Spartan military acumen, I found that they fell back on hoplite battle as what they meant by that.

This feels a bit like a motte and bailey argument to me, where a push back on overall military competence gets rebutted with a much smaller claim. Maybe the people who defend the bailey (Spartans were awesome at war) are separate from those that defend the motte (Spartans were good at hoplite battles), but it’s hard to say.

In any case, I want to be clear about what question I’m trying to answer. I just want to know if Spartans won more battles than they lost.

If Spartans won most of the battles they fought, then I have to admit that they were better than their contemporaries. If they lost most of their battles, then they weren’t. If it was about 50/50, then maybe they were only average.

There’s a lot of minutiae that goes into this, because battles are never clean competitions between comparable forces. The Spartans that are most renowned were those who went through the agoge schooling (called Spartiates), but many in Spartan forces were helots who hadn’t had that training. How do we gauge those differences?

Similarly, Sparta often went to war alongside allies. Depending on time period, they allied with the Thebans, the Athenians, the Persians, etc. If we want to know how good the Spartiates were, we should discount battles where most of the soldiers on the Spartan side were from allied forces.

We should also look at how the Spartans actually won their battles. If they won pitched battles against a numerically superior opponent, then that’s good evidence that they were strong warriors. If they won against a surprised force that was much smaller than them, I’d take that as not arguing for their skill at arms.

Spartan military might waxed and waned over time. To do this right, we should give the most weight to the battles when they were strongest.

But all of that sounds like a lot of work. So I’m going to take a list of Spartan battles (this one from wikipedia), and just look at win/loss record. I think that’ll give a good first order approximation to their abilities. I’ll look at a few individual battles after that to get a sense for the more specific questions.

Overall Battle Performance

I made a table from Wikipedia’s list of Spartan battles, and you can find it at the end of this post.

I’m not a historian, and I don’t have the decade+ to become one to answer a question that is pure curiosity on my part. It seems pretty likely that the Wikipedia list isn’t comprehensive, but my naive estimation is that it probably contains the more well known and impactful of Sparta’s battles. If you know of a better list, let me know and I might update my analysis later (time permitting).

There were 35 battles on that list. Of those, they had 16 wins, 16 losses, and 3 ties. To me, that seems to indicate that they were mostly fighting people who were about as good at war as they were. By this measure, they certainly weren’t terrible at war (as I maybe mis-interpreted Acoup as saying). On the other hand, they aren’t the gods of war that pop-culture makes them out to me.

Individual battles

Having looked at how the Spartans did overall, it will also be instructive to look at a few individual battles and see why the Spartans won or lost. Here are a few important ones:

Battle of the 300 Champions

I find the battle of the 300 champions very useful for this argument. Sparta and Argos were going to war, but they didn’t want to waste all their armies. They decided they’d have 300 men of each side fight, and that would determine who won the battle. The rest of the militaries withdrew to prevent interference, so it was really just these two groups of 300 people each.

I’m not sure who was chosen to be in the Spartan group of 300, but it seems a safe assumption that it was primarily Spartiates. Those Spartans who had been through the Agoge and were the best warriors Sparta had to offer.

This gives one of the most pure comparison points available for Sparta’s military prowess (at least as of 546BC). It’s a pitched battle between equal numbers of people, so obviously whoever wins is better at battle.

But it infamously came down to a tie. Technically two Argos soldiers survived and one Spartan soldier survived. This argues pretty strongly against the Spartan exceptionalism theory.

On the other hand, since the outcome of the battle of 300 was so in doubt, Sparta and Argos went ahead with the full battle that they’d tried to avoid earlier. Spartans defeated the Argos in this larger battle.

Another interesting tidbit is that Argos challenged Sparta to a rematch 100 years later, which Sparta declined.

Battle of Sepeia

The battle of Sepeia, also between Spartans and Argives, was a total victory for the Spartans. The Spartans completely devastated the Argive military.

Did the Spartans win through superior skill at arms? No, the Spartans ambushed the Argives while they were all eating lunch.

I don’t want to knock this tactic. All’s fair in war, as they say. But it doesn’t seem to be strong evidence that the Spartans were great hoplite soldiers, as it’s much easier to destroy an opposing force when their hands are full of food instead of weapons.

The Athenian Sicilian Expedition

During the Peloponnesian War, the Athenians invaded Sicily. Over the course of the expedition (which involved many battles), the Spartans and their allies completely destroyed the Athenians’ expedition.

Athens lost 10000 hoplites and 30000 oarsmen. That was a huge blow to their military. As Wikipedia says, “the defeat of the Sicilian expedition was essentially the beginning of the end for Athens”. After this defeat, many previously neutral parties allied with Sparta.

In a counterfactual world where Athens hadn’t invaded Sicily, they may have won the Peloponnesian War. Even if they had invaded, if they’d withdrawn when they realized they were losing they could have saved some of their soldiers to fight in later battles. My (naive) reading of this battle is that Sparta would have had a much tougher time winning the war if Athens hadn’t been defeated here.

Should we give Sparta the credit for this? There were definitely Spartans involved in the Sicilian fight against Athens. It’s hard to get a sense for numbers here, but my take on the Wikipedia article is that it was mainly Syracusans who fought off the Athenians, and they were just assisted by the Spartans. In other words, the Syracusans may have been one of the main reasons that the Spartans won the war.

The Spartan Mythos

Based on that list of battles, I have to revise my original assumptions. Spartans weren’t terrible at war. They also weren’t obviously superior at it. If I had to summon a warrior through time to organize my assault against a great evil, it’s not clear I should choose a Spartan over an Argive (I would obviously choose Alexander the Great, a Macedonian).

Why then is Sparta held up as a core of military mastery? I honestly think it’s because they liked war so much. They had a whole school devoted to teaching their kids to be warriors. It might not have helped them to conquer and hold their neighbors (which they obviously wanted to do). It did impress all of their neighbors though, and it made it clear what Sparta valued.

People in middle class America don’t fight hoplite battles. When we go to war, we have the best equipment and the most people. Our soldiers don’t necessarily need to emulate great generals or ancient soldiers, they just need to have values that work well with military discipline. Our civilians don’t even need that much, they mostly just want to feel connected to a sense of physical pride and motivation. The Spartan mythos provides these things, even if it doesn’t have much to do with Sparta itself.

I also think the Spartan mythos was pretty useful to Sparta itself. It seems pretty clear that Sparta was drinking it’s own koolaid. A friend asks the very reasonable question:

“The Spartans were, by all accounts, backwards, agrarian and few in number. But they seem to have had an outsized influence in the geopolitics of the day.”

I think recent American politics have shown that you don’t necessarily have to be skilled and exceptional to have a big impact on something. What really worked for Trump was just a willingness to push for what he wanted, and keep pushing regardless of what other people said or who might have been a better fit. It seems pretty clear the Spartans would have supported that mindset.

Table of Battles

Battle	Year	Opposition	Num Spartiates	Num Spartan Allies	Num Opposition	Result (win/tie/lose)
300 Champions	546	Argos	300	0	300	tie
Amphipolis	422	Athens	2000	2800+	1500	win
Platea	479	Achaemenid	10000	28700	100000	win
Coronea	394	Thebes	1000	14000	20000	win
Deres	684	Messenia	?	0	?	tie
Dyme	226	Achaean League			win
Fetters	550	Arcadians				lose
Great Foss	682	Messenia				win
Gythium	195	Rome+Achaean League	?	0	50000	lose
Haliartus	395	Thebes				lose
Hysiae	669	Argos	?	?	?	lose
Hysiae	417	Argos				win
Lechaeum	391	Athens	600	0	?	lose
Leuctra	371	Boeoteans+Thebans	12000		18500	lose
Lyncestis	423	Illyrians+Lyncesteans	<3000	1000+	?	tie
Mantinea	207	Achaean League			lose
Mantinea	362	Boeoteans+Thebans			lose
Mantinea	418	Argos+allies	3500	5500	8000	win
Megalopolis	331	Macedonians	22000	?	40000	lose
Lycaeum	227	Achaean League			win
Munychia	404	Athenian Rebels	5000	?	1000	lose
Nemea	394	Athens+allies	6000	12000	24600	win
Olpae	426	Athens+allies	2000	3000	10000	lose
Orneae	417	Athens+Argos	?		1200	lose
Phyle	404	Athenian Rebels	700+cavalry		700	lose
Piraeus	403	Athenian rebels			win
Platea	429	Platea	?	?	?	win
Sellasia	222	Achaean League	20650		29200	lose
Sepeia	494	Argos				win
Sicilian Expedition	415	Delian League	1000	1200cavalry+100ships+??	12000+ships	win
Mantinea	385	Arcadians	?	?		win
Sparta	272	Epirus	0	9000	27000	win
Sphacteria	425	Athens	440	0	3000	lose
Tanagra	457	Athens	1500	10000	14000	win
Tegyra	375	Thebes	1800	0	500	lose

There are a lot of uncertainties about the result of a nuclear war, but one thing seems clear: it would be bad. How bad depends on things like who we go to war with, number of nuclear weapons used, weather patterns, etc. Wikipedia documents some estimates that the US government produced during the cold war as saying that nuclear war with the Soviet Union could lead to the death of 70% of all Americans. My wife and I have two kids. If 70% of us die, that’s three out of the four people in our family. My kids, my wife, gone.

Since the cold war, the number of nuclear weapons stockpiled has been reduced by about 85%. That said, there are over ten thousand nuclear weapons in the world, over half operated by other countries. Things would still be very bad if we got into a nuclear war.

In a lot of ways, I see nuclear war deterrence as one of the more important responsibilities of a US president. It doesn’t matter what other policies they put in place if they get us involved in a war that kills 70% of Americans. I want a president that will continue drawdown of current nuclear stockpiles, prevent other countries from continuing their nuclear weapons programs, and provide stability to the international environment. That’s one part of why I’m going to vote for Biden.

As President, Donald Trump has spent the last four years making our country much less safe from nuclear war. It can be hard to evaluate some of the nuclear decisions his administration has made, given the international landscape. Unilateral disarmament seems likely to make the US less safe, and modernizing our nuclear arsenal improves reliability and safety. Because of that, we have to look at all of the administration’s decisions as a whole to determine if they’re improving the security of Americans.

The Trump administration has:

• actively called for development of new nuclear weapons (both in type and in quantity).
• focused on increasing capabilities to match Russia and China, instead of negotiating for more international drawdown
• broadened the definition of “extreme circumstances” under which nuclear weapons could be used
• pulled out of the INF. This was done because Russia wasn’t meeting targets, but the INF governed more than just the US and Russia. Pulling out of the INF reduces leverage on other nuclear powers governed by the treaty, as well as those not officially in the treaty but who abided by it (like Germany and Slovakia).
• introduced development of low-yield nuclear weapons
• looks likely to not extend the New START treaty, which places limits on the number of nuclear weapons Russia and the US can deploy. Russia is currently complying with that treaty.

In addition to leaving nuclear non-proliferation treaties and calling for development of new nuclear weapons, the Trump administration has also completely failed to reign in North Korea and Iran.

North Korea currently has around 30 nuclear weapons and can produce something like 6 more weapons each year. Several years ago, North Korea offered to start reducing nuclear capabilities in exchange for lifting of sanctions, but Trump walked away. A couple months ago, North Korea said that negotiating with Trump had been “a nightmare” and that they were going to increase their nuclear weapons stockpile.

Iran’s nuclear weapons development had, prior to Trump’s election, been governed by the JCPOA. The JCPOA was an agreement between Iran, the US, and several other nations. It governed how Iran was to eliminate its stockpile of enriched uranium. Iran would still be able to build nuclear power plants, but not to enrich enough to build nuclear weapons. In 2018, Trump’s administration withdrew from that agreement over the protest of every other member (including Iran). After the US withdrew, Iran and the other countries in JCPOA attempted to continue abiding by the agreement. The US’s withdrawal from JCPOA led to series of skirmishes which culminated in the US killing an Iranian major general. In response to that killing, Iran has said that they won’t abide by the JCPOA at all. By their actions, the Trump administration increased the likelihood of Iran getting nuclear weapons.

Let’s contrast with Biden. Biden wants to extend the New START treaty. He wants to drawdown nuclear stockpiles. We have evidence from his decades in politics of him working to reduce the likelihood of nuclear war. Biden has also released a letter describing his approach to nuclear disarmement treaties in the past.

This quote in particular is why I think Biden will manage our nuclear policy well:

“Despite what some extreme voices argued at the time, the arms control agreements we hammered out with the Soviets were not concessions to an enemy or signs of weakness in the United States.
They were a carefully constructed barrier between the American people and total annihilation.”

Joe Biden

It’s pretty common these days to talk about how much Jeff Bezos could buy for us. Facebook and twitter are both full of people saying things like this:

The idea being that if Jeff Bezos just paid his share of our country’s upkeep, we could have a utopia.

There’s a problem with this idea, but it’s not a political problem. It’s a math problem. It’s a problem with what people mean when they say “wealth” or “taxes”.

He doesn’t have the cash

First thing’s first: Bezos has somewhere around $200 Billion now (a quarter of his and MacKenzie Scott’s wealth went to her in the divorce). That wealth is not cash in a bank account. It’s Amazon stock that he owns. There’s no way for him to spend that much money, because he doesn’t have it as money.

If we wanted to take our 4.7% of his wealth, we’d have to start by selling about $10B worth of his Amazon stock. Selling that much stock would have an impact on Amazon’s stock price, so we’d likely have to sell more shares than you’d expect to reach that amount.

Bezos spends around $1Billion a year on his new space company, Blue Origin. He makes a big deal about that, I think, in large part because he has to justify selling that much stock every year. If Bezos just started selling Amazon stock for no reason, especially that amount, the price of the stock would plummet and he’d lose a lot of his wealth. People would assume that he knew something bad about Amazon’s business.

Now if he were selling the stock to pay for College For All, that would be a pretty good signal to the market that Amazon was still a stable company. The market price for the stock likely wouldn’t drop much from our $10B sale due to a lack of confidence.

I was originally going to write something here about $10B being a lot to sell on the stock market, but it turns out that’s not true. The NASDAQ (where Amazon is listed) clears over $100B per day. Bezos could probably find someone to buy his $10B of stock pretty easily.

Normal US Taxes don’t work like that

Let’s say that we decide it’s a good idea. That $10B that people are paying Bezos for his stock wasn’t doing us any good before (it was probably just wrapped up in some other big tech stock). We’re going to have Bezos fund our College.

The thing is, we can’t do this by just taxing Bezos normally. The US has an income tax. That’s a tax on income. Bezos actually doesn’t have much income, he just has assets that are worth a lot. This means that if President Biden (I hope that’s who we have next year!) says that 2021 will have a super high tax on everyone named Jeff Bezos, we wouldn’t actually get much money.

Jeff Bezos doesn’t pay any taxes on his stock until he sells it, and then he only pays taxes on the appreciation. Though given that he got the stock when it was likely worth a single dollar, the tax will apply to pretty much the entire amount he’s selling.

So if Bezos did sell $10B in stock next year, then we’d only be taxing that $10B. The current capital gains tax would be 20% for him, so we’d only get $2B from that sale.

In order to fix this, we’d need to tax wealth, not income. We could absolutely do that, and Piketty has advocated for that kind of tax to help deal with some of the social problems that we’re facing now. But I don’t really think that Jack Califano, from our original tweet up above, is thinking about it like that. Obviously I don’t know what his understanding of our current tax situation is, but if he were proposing something as radical as a wealth tax I’d have expected him to play it up.

Math vs. Politics

Enough of this tax bracket, stocks-vs-cash nonsense. We want our College For All; let’s get Bezos to pay for it. We’re going to pass a law that says Bezos has to sell enough stock every year to provide 4.7% of his wealth to the US government, each year, effective immediately.

Tomorrow, Bezos sells enough stock to get a grand total of $10B from it (remember that his current wealth is around $200B, so 4.7% is slightly less than $10B). Now can we all have free college?

No, no we can’t. Because Bernie Sanders says that he needs $48B per year to pay for his College For All plan. I have no idea where Califano got the 4.7% number, but it makes no sense. Bezos could only pay for College For All for four years, even if we gave him a wealth tax of $50B/yr.

Bezos has a lot of money, but he doesn’t have that much.

Why

I’m sympathetic to Califano’s argument. It would be really nice for Bezos to pay to improve America. Hell, it would be nice for him to pay to improve Seattle (more directly than he’s doing by building nice buildings and bringing in employees who spend money). People have been trying to get Amazon to pay more Seattle taxes for a long time, and I hope that they’ve finally managed it.

I’m a bit more reluctant about the idea of a wealth tax, but I could be convinced by the right arguments and experiments.

I want free college (and free healthcare, and affordable housing) for everyone in America. I want it so bad that I’m willing to pay attention to reality to find ways to get it. This is why I get so frustrated when people start talking about having Bezos pay for everything.

Bezos has a lot of money, but he doesn’t have that much. Simple “tax the rich” schemes also generally won’t access most of his money, so saying that we should tax Bezos without specifying that you want to totally change the way taxes are done in America seems disingenuous.

I want people to work towards a better world together. To do that, we all need to know what direction a better world is. If we just ignore the math, I’m afraid of where we’ll actually end up.

I read Achtung Baby, by Sara Zaske, when my kids were about six months old. The book is part travelog, part parenting advice, by a woman who moved her family from the US to Germany. She raised kids for five years there, came back to the states, and wrote a book on the difference in parenting cultures.

One of the biggest things that stuck with me about this book was the discussion about Einschulung, and life milestones parties more generally. An Einschulung is a party thrown for a kid when they first go off to school, and it is a big deal. Everyone is invited, family, extended family, friends, neighbors. Everyone comes out to celebrate and acknowledge this major milestone for the kid.

The Einschulung is compared with two other major parties that Germans have in their lifetimes: their Jugendweihe celebrating entrance into young adulthood and their wedding. These are the three parties that define the arc of many a German’s life, and they help tie the person into their community.

Community

What struck me most about the Einschulung, Jugendweihe, and wedding is how they were seen in Germany. Or perhaps how Sara Zaske saw them. These were parties that were in honor of a given person, but not always for them. Often the parties were for the community that person belonged to as much as they were for the person themselves.

This really appealed to me when I was reading it as a new parent. I still had fresh memories of my own wedding two years before, and how my wedding had changed my views on weddings overall. Prior to my own wedding, I’d often viewed wedding invites with distaste. When some friends got married, I’d feel obligated to go in order to show my support, but I often felt pretty isolated at weddings. I didn’t know how to interact with the event, or the people at the event.

When planning our wedding, my wife and I wanted to really emphasize the family and community aspects. We ended up doing a lot of non-standard wedding things, but the closer we got to the wedding, the more those seemed to matter less to me than having people there to witness our love. I think several of our plans for our wedding were amazing, and a couple fell kind of flat, but the thing that was most meaningful to me was just having so much family and so many friends there with us as we said we loved each other.

I really understood then that our wedding wasn’t just for us, it was for our community as well.

This was a pretty new experience for me. I was a lonely kid, and had a lot of trouble making friends. It wasn’t until I was in my mid-twenties that I understood that it was possible to have a social interaction with someone new that wasn’t emotionally painful. My wedding was the final push I needed to see community in a different way.

Reading about Einschulung in Achtung Baby got me wondering if I could have had a much more socially comfortable adolescence if I were raised in a culture that emphasized community in a more formal way. It’s really too bad the US is the way that it is, but maybe I could do something like that for my kids anyway.

Other states

I was pretty surprised to discover that, at least in one US state, there are parties like Einschulung. Several Michiganders that I know recently told me about the tradition of high school graduation parties there.

In Michigan, everyone apparently throws a high school graduation party. You invite your family, your friends, your friends’ families, your neighbors, your parents coworkers. It’s a regular community ritual. It’s such a big deal that high schoolers carefully schedule their graduation parties to not overlap with their classmates, so that everyone can go to everyone else’s parties.

I was immediately excited about this and wondering if Michiganders felt less isolated and more tied in to their community than I had as a high schooler.

Not Always Good

It turns out that one of the people who was telling me about this tradition had hated their graduation party. They felt that it was a party for their parents, not for them, and that they were being forced to go. In fact, the way they described it reminded me a lot of how I felt about other people’s weddings before I’d had my own.

This raises some interesting questions. Why hadn’t I felt like I was a part of a community when I was going to other people’s weddings before I had my own? Why did my friend wish they hadn’t had a high school graduation party, instead of feeling like it was their community supporting them?

It’s hard to speculate on my own about what someone else was feeling at some party, but I think my own lack of community feeling was related to a sense of support going one way only. I went to weddings of friends and families because I wanted to be there for them, which is actually a large part of what I consider to be a good community. But I didn’t feel communal about it, I felt like it was an obligation. I was doing it to avoid being cast out of my community, not because I wanted to build a stronger community. I don’t think I even had a sense that community could benefit me in any way.

This is not to say that community never benefited me before I got married (though the amount of community support I received after my wedding was mind boggling). Looking back, I see many times when my community was supporting me throughout childhood and young adulthood. My experience of that support at the time was confused though. People would do something nice for me, and I wouldn’t understand why. I’d feel like I had to pay them back immediately, or that they were condescending to me. It also wasn’t clear to me if someone was “in my community” or not (a question not at all helped by the introduction of Facebook).

This makes me wonder if my wedding was a turning point because it really shoved my face in the idea that other people were helping me because they wanted me to be happy. Planning and throwing a wedding is not an easy thing, and there’s often a ton of family stress on top of that. We never would have been able to throw the wedding that we did without the help of a huge number of people.

I think this is why the other two parties described in Achtung Baby sounded so good to me. If I’d had the idea that other people might genuinely want to help me when I was a kid, or that they might actively want me to be a part of their community, then I would have had a much happier childhood. The Einschulung seems like a very stark demonstration of that fact to a kid when they could most use it: right before joining a huge group of people they’ve never met before to do something totally new.

Celebrating With My Kids

This idea of the reason behind community parties offers up some ideas for how to do similar things for my kids as they age:

1. throw parties at milestones that are a Schelling Point for the community that you’re in
2. let people help with party set up in a way that’s visible to others
3. invite everyone that’s in your community, but not everyone you know
4. make sure the party will actually be enjoyable for the kids

I think point 4 is pretty important. I really enjoyed my wedding, and I suspect I’d be feeling differently about community if I hadn’t (even if my community had been exactly as helpful). I also suspect that this was what went wrong for my friend who hated their own graduation party. If the party had been structured more to their liking, then they could have recognized the community aspects of it more easily.

I also think point 1, about choosing milestones that make sense for your community, is important. This makes me think that birthdays are more important than I had been thinking before this, and going forward I plan to place more importance on my kids birthdays and on my own birthday.

Last month, I started experimenting with AcesoUnderGlass’s Knowledge Bootstrapping method. I started out with a small project learning some facts about radiation and electronics. That worked well, so I then went to learn about something a little less straightforward: GPT-3’s likely impact on AI safety.

I have to be honest, selecting this topic may have been a bit of a mistake. I was seeing a lot headlines and posts about GPT-3, and I had a pretty immediate emotional reaction of “GPT-3 isn’t a big deal and people don’t know what they’re talking about.”

I had a lot of fun writing this post, but I’m less happy with the final product than I expected to be. The thing is, I had that original emotional reaction to a bunch of headlines. I literally hadn’t read the articles before I had decided to try to rebut them. When I went to go read the articles themselves, they were different than lots of the headlines and twitter hype had implied (shocking, I know). As I read more about GPT-3, I ended up changing my mind several times about my thesis. The post I wrote was much different than the one I was planning on.

In a lot of ways, this is great. I learned a lot about the current state of AGI research, and some of the current major players in AI safety. Deciding (before doing any research) to write a post about the topic is what gave me the motivation to actually read all those articles, and then read the background, and then read even more background. I haven’t really kept up with these things for the past three years, so things had changed a lot since I had last looked into it. This project gave me the push I needed to finally learn how the transformer architecture really worked, as well as uncovering some of what DeepMind has been doing. I hadn’t even known that MuZero existed before starting on this project.

Motivation

All of this leaves me still excited about the knowledge bootstrap method, but I’m also noticing that keeping my motivation for a research project up is hard. When I have a blog post that I’m excited about writing, it’s easy to put in effort to learn and write. When someone is wrong on the internet, of course I’ll be burning to write about it. The more I wrote my post, the more clear it became that I was the one wrong on the internet.

That started sapping my motivation to write, even though the things that I was writing changed enough that I still stand by their accuracy.

As I closed in on answering most of the questions that I had come up with in my original question decomposition, I had such a different understanding of the topic that I realized I had an enormous number of new questions. I answered those questions, and then the questions that followed from that. Eventually, I came to the point where I thought I had a decent stance on the original safety question I had. At that point, I also realized how much detail there was to making a decent prediction about GPT-3’s implications on future safe AI. And much of that detail was (and is) still unknown to me.

As I began to realize how much I’d have to research in order to do the topic justice, I could feel my excitement fade. Given that I’ve had a very stuttering relationship with this blog over the past decade or so, I could recognize that if I let my excitement about the topic drive me into perfectionism I wouldn’t post anything. I also recognized that if I didn’t post that blog entry, I’d feel like a failure and there would be a long drought in me posting anything at all.

I decided that I had enough for a high level post and wrote it, but I ended up writing a more milquetoast thesis than I had originally intended.

The most important thing for me in any kind of learning project is keeping up motivation. For work related topics, there’s enough external motivation that I can power my way to a solution one way or another. For personal projects, even personal projects that could help me out at work, I need to stay interested throughout the process to have any hope of success.

My first experience of Knowledge Bootstrapping showed me that an emphasis on questions could help me keep my motivation up. By keeping my thoughts close to my original questions, it was easy to remember why I was doing the thing. This second experience of the process showed me that the blog output itself is still a big part of my motivation, and I’ll need to plan around that in future projects.

Question Decomposition

I still view question decomposition as one of the more important components of Knowledge Bootstrapping. My original project had a very straightforward set of questions, and after I decomposed them it was easy to pull answers out of the sources I found. The hardest part of my Radiation+Electronics mini-project was finding sources that went deep enough to truly answer my questions.

The GPT-3/AI-safety mini-project was much different. When I first started decomposing questions (before I started doing much reading) I had a ton of trouble figuring out what my primary question even was. Then I had trouble breaking that down into questions that reading books/papers could answer. I did my best to decompose the questions, then went and tried to answer them. That helped me orient myself to the field again, and when I came back to try answering my original questions I could clearly see some better question decompositions.

I ended up iterating this process several times, and I think for difficult or new topics this is probably crucial.

Elizabeth says that if you’re not sure what notes to take when you’re reading a source, you should go look at your questions again. That isn’t great advice if you’re having trouble with the decomposition step itself. I tried to address this by emphasizing the difference between what I was reading and what I already thought, and writing that down. That also helped me to figure out what my questions were, as I would sometimes realize I disagreed with something but be uncertain why.

Pre-Read, Brain-Dump

Elizabeth emphasizes doing a brain dump of what you think about any given source before you really start reading it. I didn’t do this very much in my first mini-project, but I did it for every source in this project.

I now think that my radiation+electronics mini-project didn’t need much of the brain-dump step because I’d been thinking about the topic on and off for several years. I pretty much knew what I already knew. I also had a mindset that was focused on fact acquisition and model building, but I didn’t have to worry much about conflicting information or exaggeration.

With GPT-3 and AI safety, there’s no settled science about the topic. Everything is new, so people are all very excited. That meant that I had to be more careful with what sources I was using. I also didn’t have a good handle on what questions I was trying to answer at the beginning, which meant that it was harder for me to notice what was important about each source’s content.

This is where the pre-read brain-dump really shines. Before I did an in-depth read of any source, I’d free-write for a while about what I expected the source to say. I’d also write about what I personally thought about the expected content of the source. Then when I went to read the source, it was easy for me to notice myself being surprised. That surprise (or disagreement, or whatever) was the trailhead for the questions that I should have been asking at the beginning.

Interestingly, this seems to be the exact opposite of the reason that Elizabeth does it. She talks about how, if she didn’t get her brain dump on paper, those thoughts would be floating around her head interrupting her reading process.

When I don’t do the brain dump, I don’t have any of those thoughts floating around my head as I read. That makes it really hard for what I read to latch on to what I already know. I’ll sometimes read something and feel like I understand it, but then be unable to recall it even ten minutes (or ten pages) later. By brain-dumping, I prime my mind with all those thoughts so that I’m actually engaging with and thinking about the content in the source.

(Though Elizabeth also talks about this a bit here, where she says breaking the flow of a book is a sign of engagement).

In the past I’ve tried to address this with Anki. When I was reading textbooks cover to cover, I’d create flash cards of the major things I learned. This was generally very effective, but I’ve ended up with a truly enormous number of cards. I haven’t kept up on my Anki training for the past couple weeks, and I now have hundred of cards in my backlog. It’s also pretty slow to do this, and really takes me out of the flow of reading.

A good future workflow might be something more like:

1. question decomposition
2. source selection
3. brain-dump
4. read and note take
5. post-process notes and write blog post
6. generate anki cards that are more focused

Tools

One of the things that held me back during my first Knowledge Bootstrapping mini-project was being unfamiliar with some of the markdown features that Elizabeth makes common use of. Because of that, my writing project was slower and more awkward than I think is Elizabeth’s experience.

I took some time (really just ten minutes or so) to look up some of the markdown features that I had wanted to use in my first project. Using those made this second project a lot easier. I was a lot more comfortable drafting the post and referring to each source. I’m beginning to see how the process itself could become more natural and get in the way less.

I still feel pretty curious about Elizabeth’s actual workflow during note-taking and synthesis though. She described it at a high level in her post, but I’m more interested in the nitty-gritty at this point. What does she make a tag, and why? How does she manage her tags? Does she really actually use that many of them?

I was playing around with robot localization the other day, and realized that the angular degrees of freedom a robot has follow an interesting pattern. A robot that can just move around a floor has only one degree of angular freedom; it can rotate to the left or right. A flying robot, on the other hand, has three angular degrees of freedom: it can pitch, roll, or yaw.

That made me curious how the number of angular degrees of freedom is related to the number of spatial degrees of freedom. If we could build a robot that could move in the 4th spatial dimension, how would it rotate?

A robot that can only move along one line is the degenerate case. This one dimensional bot has a single binary degree of freedom in rotation. It can point either forward or backwards.

A robot that can move in a single plane, like a roomba, has a single angular degree of freedom in rotation. It can rotate however it wants as long as it remains parallel to the floor.

A robot in arbitrary three space has the traditional angular degrees of freedom of roll, pitch, and yaw.

But what about a robot in arbitrary spatial dimensions? What would a robot’s degrees of freedom look like in 4-D space, or n-D space?

As normal, the linear degrees of freedom equal the dimensions of the space. So in n-D space there are n linear degrees of freedom.

At first, I naively thought that the number of angles the robot could rotate around would be the number of axes also. After all, in three spatial dimensions there’s one orthogonal axis for each plane the robot rotates in. But for higher dimensional cases this doesn’t quite follow. The plane that’s defined by being orthogonal to one axis is actually a hyperplane. It’s made up of all (n-1) dimensions at a right angle to the axis of rotation. If our robot sensors are still just 2D or 1D devices, then we probably want to be more precise about what plane they’re rotating in.

What we’re interested in for robot rotations is (I think) the number of 2D planes that the robot could rotate around. Just by happenstance, the number of 2D planes in 3-space is the same as the number of axes. But for higher dimensional spaces we actually have to define the 2D plane by choosing two orthogonal vectors and finding their span. We can find a sufficient set of planes by choosing orthogonal vectors that are all aligned with an axis of the space.

So the number of 2D planes in an nD space is {n \choose 2}, or \frac{n!}{(2*(n-2)!)}. Here’s a list of the number of 2D planes of rotation for a few different numbers of spatial dimensions:

• 2D = 1 plane of rotation
• 3D = 3 planes of rotation
• 4D = 6 planes of rotation
• 5D = 10 planes of rotation
• and so on

Edited 2020/08/31 to remove an erroneous RNN comment.

I spent about six months in middle school being obsessed with The Secret Life of Dilly McBean by Dorothy Haas. It’s a book about an orphan whose mad scientist parents gave him super magnetism powers before they died. When the book opens, he’s been adopted and moved into a new town. Many magnetism adventures follow, including the appearance of some shadowy spy figures.

After many exasperating events, it’s finally revealed that (spoiler) the horrible no-good Dr. Keenwit is trying to take over the world. How, you might ask? By feeding all worldly knowledge into a computer. Dr. Keenwit would then be able to ask the computer how to take over the world, and the computer would tell him what to do. The shadowy spy figures were out collecting training data for the computer.

Middle school me got a great dose of schadenfreude at the final scene where Dilly runs through the rooms and rooms of magnetic tape drives, wiping all of Dr. Keenwit’s precious data with his magnetism powers and saving the world from a computer-aided dictator.

GPT-3

Dr. Keenwit would love GPT-3. It’s a transformer network that was trained on an enormous amount of online text. Given the way the internet works these days, you could round it off to having been trained on all worldly knowledge. If Dr. Keenwit had gotten his evil hands on GPT-3, would even Dilly McBean have been able to save us?

The internet has been flooded with examples of what GPT-3 can (and can’t) do. Kaj Sotala is cataloging a lot of the more interesting experiments, but a few of the biggest results are:

• working automatic code generation from english descriptions
• medical diagnoses
• image generation
• writing any kind of text

How is it doing those things? Using all of that source text, GPT-3 was trained to predict new text based on whatever came before it. If you give it the first half of a sentence, it will give you the second half. If you ask it a question, it will give you the answer. While it’s technically just a text prediction engine, various forms of text prediction are the same as conversation. It’s able to answer questions about history, geography, economics, whatever you want.

Even Tyler Cowen has been talking about how it’s going to change the world. Tyler is careful to reassure people that GPT-3 is no SkyNet. Tyler doesn’t mention anything about Dr. Keenwit, but I have to guess that he’s not worried about that problem either.

GPT-3 isn’t likely to cause the end of the world. But what about GPT-4? Or GPT-(N+1)?

GPT-3, on it’s own, just predicts text. It predicts text like a human might write it. You could give it 1000 times more NN parameters and train it on every word ever written, and it would still just predict text. It may eventually be good enough for Dr. Keenwit, but it’ll never be a SkyNet.

Agents

We don’t have to worry about a GPT SkyNet because GPT isn’t an agent. When people talk about agents in an AI context, that means something specific. An agent is a program that interacts with an environment to achieve some goal. SkyNet, for example, is interacting with the real world in order to achieve its goal of world domination (possibly as an instrumental goal to something else). Dr. Keenwit is interacting with society for the same goal. All people are agents, not all programs are agents.

This isn’t to say that GPT-N couldn’t be dangerous. A nuke isn’t an agent. Neither is an intelligence report, but that intelligence report could be very dangerous if read by the right person.

But GPT is a bit more worrisome than an intelligence report or a history book. GPT can interact with you and answer questions. It has no goal other than predicting text, but in the age of the internet text prediction can solve an enormous number of problems. Like writing working software.

If you give GPT an input, it will provide an output. That means that you could feasibly make it into an agent by piping it’s text output to a web browser or something. People are already proposing additions to GPT that make it more agent-y.

The thing is, GPT still has only one goal: predicting human generated text. If you give it access to a web browser, it’ll just output whatever text a human would output in response to whatever is on the page. That’s not something that’s going to make complicated take-over-the-world plans, though it might be something that talks about complicated take-over-the-world plans.

What if we build structure around GPT-n to turn it into an agent, and then tweak the training objective to do something more active. Do we have SkyNet yet? Steve2152 over at LessWrong still doesn’t think so. He comes up with a list of things that an Artificial General Intelligence (like SkyNet) must have, and argues that GPT will never have them due to its structure.

Steve2152’s argument hinges on how efficient GPT can be with training data. The GPT architecture isn’t really designed for doing things like matrix multiplication or tree search. Both of those things are likely to be important for solving large classes of problems, and GPT would be pretty inefficient at doing it. The argument then analogizes from being inefficient at certain problems to being unable to do other problems (similar to how standard DNNs just can’t do what an RNN can do).

Instead of using a transformer block (which GPT uses), Steve2152 would have us use generative-model based AIs. In fact, he thinks that generative-model based AI is the only thing that could possibly reach a generalized (AGI) status where it could be used to solve any arbitrary problem better than humans. His generative-models seem to just be a group of different networks, all finding new ideas that explain some datapoint. Those models then argue among each other in some underspecified way until one single model emerges the winner. It sounds a lot like OpenAI’s debate methods.

I’m not convinced by this generative-model based argument. It seems too close to analogizing to human cognition (which is likely generative-model sub-agents in some way). Just because humans do it that way doesn’t mean it’s the only way to do it. Furthermore, Steve2152’s argument equates GPT with all transformer architectures, and the transformer can be used in other ways.

Transformers, more than meets the eye

Obviously an AI trained to generate new text isn’t going to suddenly start performing Monte Carlo Tree Search. But that doesn’t mean that the techniques used to create GPT-3 couldn’t be used to create an AI with a more nefarious agent-like structure. Standard DNNs have been used for everything from object recognition to image generation to movie recommendations. Surely we can reuse GPT techniques in similar ways. GPT-3 uses a transformer architecture. What can we do with that?

It turns out we can do quite a lot. Nostalgebraist has helpfully explained how the transformer works, and he’s also explained that it can model a super-set of functions described by things like convolutional layers. This means we can use transformers to learn even more complicated functions (though likely at a higher training expense). The transformer architecture is much more generalizable than models that have come before, which I think largely explains its success.

If we wanted SkyNet, we wouldn’t even necessarily need to design control logic ourselves. If we connect up the output of the GPT-3 architecture to a web browser and tweak the cost function before re-training, we could use the same transformer architecture to make an agent.

It’s not even clear to me that the transformer will never be able to do something like tree search. In practice, a transformer only outputs one word at a time. When you want more than one output word, you just repeat the output portion of the transformer again while telling it what it just output. (You can get a good example of what that looks like in this explainer). If you train a transformer to output sentences, it’ll do it one word at a time. You just keep asking it for more words until it says that it’s done by giving you an “end” symbol. It seems possible to use this structure to do something like tree search, where the output it gives includes some kind of metadata that lets it climb back up the tree. You’d never get that with the training corpus that GPT-3 uses, but with the right training data and loss function it seems feasible (if very inefficient).

But if we’re really worried about being able to do tree search (or some other specific type of computation) in our future SkyNet, then maybe we can just put that code in manually.

AlphaGo to MuZero

Hard coded agent-like structure is a large part of what made DeepMind’s AlphaGo and it’s descendants so powerful. These agents play games, and they play them well. AlphaGo and AlphaZero set world records in performance, and are able to play Go (a famously hard game) at superhuman levels.

The various Alpha* projects all used a combination of the game rules, a hand-coded forward planning algorithm, and a learned model that evaluated how “good” a move was (among other things). The planning algorithm iteratively plans good move after good move, predicting the likely end of the game. The move that is predicted to best lead to victory is then chosen and executed in the actual game. In technical terms, it’s doing model based reinforcement learning with tree-search based planning.

By changing what game rules AlphaZero used, it could be trained to superhuman levels on Chess, Go, or Shogi. But each game needed the game rules to be manually added. When it needs to know where a knight would be allowed to move, AlphaZero could just consult the rules of chess. It never had to learn them.

Now DeepMind has released a paper on MuZero, which takes this to a new level. MuZero learns the game rules along with goodness of moves. This means that you can train it on any game without having to know the rules of the game yourself. MuZero achieves record breaking performance on board games and Atari games after automatically learning how the game is played.

With MuZero, the game rules are learned as a hidden state. This is pretty different from prior efforts to learn a game model from playing the game. Before this, most efforts emphasized recreating the game board. Given a chess board and a move, they’d try to predict what the chess board looks like after the move. It’s possible to get decent performance doing this, but a game player built this way is optimizing to produce pictures of the game instead of optimizing to win.

MuZero would never be able to draw you a picture of a predicted game state. Instead, its game state is just a big vector that it can apply updates to. That vector is only loosely associated with the state of the actual game (board or screen). By using an arbitrary game state definition, MuZero can represent the game dynamics in whatever way lets it win the most games.

MuZero uses several distinct neural nets to achieve this. It has a network for predicting hidden game state, a network for predicting game rules (technically, game dynamics), and a network for predicting a move. These networks are all hand-constructed layers of convolutional and residual neural nets. DeepMind in general takes the strategy of carefully designing the overall agent structure, instead of just throwing NN layers and compute at the problem.

I’m a lot more worried about MuZero as a SkyNet progenitor than I am about GPT-3. But remember what we learned from Nostalgebraist above? The transformers that GPT-3 are based on can be used to learn more general functions than convolutional nets. Could GPT and MuZero be combined to make a stronger agent than either alone? I think so.

It’s interesting to note here that MuZero solves one of the most common complaints from writers about GPT-3. GPT-3 often loses the thread of an argument or story and goes off on a tangent. This has been described as GPT not having any internal representation or goal. Prosaically, it’s just generating text because that’s what it does. It’s not actually trying to tell a story or communicate a concept.

MuZero’s learned hidden state, along with a planning algorithm like MCTS, is able to maintain a consistent plan for future output over multiple moves. Its hidden state is the internal story thread that people are wanting from GPT-3 (this is a strong claim, but I’m not going to prove it here).

I like this plan more than I like the idea of plugging a raw GPT-3 instance into a web browser. In general, I think making agent structure more explicit is helpful for understanding what the agent is doing, as well as for avoiding certain problems that agents are likely to face. The hand-coded planning method also bootstraps the effectiveness of the model, as DeepMind found when they trained MuZero with planning turned off and got much worse performance (even compared to MuZero trained with planning turned on and then run with planning turned off).

Winning

The main follow on question, if we’re going to be building a MuGPT-Zero3 model, is what “winning” means to it. There are a lot of naive options here. If we want to stick to imitating human text, it sure seems like a lot of people treat “getting other people to agree” as the victory condition of conversation. But the sky is the limit here, we could choose any victory condition we want. Text prediction is a highly underconstrained problem compared to Go or Atari.

That lack of constrained victory condition is a big part of the AGI problem in the first place. If we’re going to be making AI agents that interact with the real world to achieve goals, we want their goals to be aligned with our own human goals. That’s how we avoid SkyNet situations, and we don’t really know how to do it yet. I think lack of knowledge about useful value functions is likely the biggest thing keeping us from making AGI, aligned or not.

If we ask whether we can get AGI from GPT or MuZero, then we get into all sorts of questions about what counts as AGI and what kind of structure you might need to get that. If we just ask whether GPT and MuZero are a clear step towards something that could be dangerous on a global level (like SkyNet), then I think the answer is more clear.

We’re getting better at creating models that can answer factual questions about the world based on text gleaned from the internet. We’re getting better at creating models that can generate new text that has long duration coherency and structure. We’re not yet perfect at that, but the increase in capability from five years ago is stunning.

We’re also getting better at creating agents that can win games. As little as 6 years ago, people were saying that a computer beating a world-champion at go was a decade away. It happened 5 years ago. Now we have MuZero, which gets record-breaking scores on Atari games after learning the rules through trial an error. MuZero can match AlphaGo’s Go performance after learning Go’s rules through trial and error. This is also a stunning increase in game playing ability.

We don’t have a good way to constrain these technologies to work for the good of humanity. People are working on it, but GPT-3 and MuZero seem like good arguments that capabilities are improving faster than our ability to align AI to human needs. I’m not saying that we need to run through the datacenters of DeepMind and OpenAI deleting all their data (and Dilly McBean’s magic magnetism powers wouldn’t work with contemporary storage technology anyway). I am saying that I’d love to see more emphasis on alignment right now.

There are a few different organizations working on AI alignment. OpenAI itself was originally formed to develop AI safely and aligned with human values. So far most of the research I’ve seen coming out of it hasn’t been focused on that. The strongest AI safety arguments I’ve seen from OpenAI have been Paul Christiano basically saying “we should just build AGI and then ask it how to make it safe.”

In all fairness to OpenAI, I haven’t tracked their research agenda closely. Reviewing their list of milestone releases reveals projects that seem to emphasize more powerful and varied applications of AI, without much of a focus on doing things safely. OpenAI is also operating from the assumption that people won’t take them seriously unless they can show they’re at the cutting edge of capabilities research. By releasing things like GPT, they’re demonstrating why people should listen to them. That does seem to be working, as they have more political capital than MIRI already. I just wish they had more to say about the alignment problem than Paul Christiano’s blog posts.

In fairness to Paul Christiano, he thinks that there’s a “basin of attraction” for safety. If we build a simple AI that’s in that basin, it will be able to gradient descend into an even safer configuration. This intuitively makes sense to me, but I wouldn’t bet on that intuition. I’d want to see some proof (like an actual mathematical proof) that the first AGI you build is starting in the basin of attraction. So far I haven’t seen anything like that from Paul.

DeepMind, on the other hand, was founded to create a general purpose AI. It wasn’t until Google bought it that they formed an internal ethics board (which apparently has a secret membership). They do have an ethics and society board (separate from their internal ethics board) that is also working on AI safety and human alignment (along many different axes). It seems like they’re taking it seriously now, and they have a fairly active blog with detailed information.

MIRI is working exclusively on AI safety, not on capabilities at all. They’ve released some papers I find pretty intriguing (especially related to embedded agency), but publicly visible output from them is pretty sporadic. My understanding is that they keep a lot of their work secret, even from other people that work there, out of fear of inspiring larger capability increases. So I basically have no idea what their position is in all this.

All of this leaves me worried. The ability to create AGI seems closer every year, and it seems like we’re making progress on AGI faster than we are making progress on friendly AI. That’s not a good place to be.

Over the last few weeks, AcesoUnderGlass has been posting a series about how to research things effectively. This culminated with her Knowledge Bootstrapping Steps v0.1 guide to turning questions into answers. To a first approximation, I think this skill is the thing that lets people succeed in life. If you know how to answer your own questions, you can often figure out how to do any of the other things you need to do.

Given how important this is, it seemed totally worth experimenting with her method to see if it would work for me. I picked a small topic that I’d been meaning to learn about in detail for years. I used the Knowledge Bootstrapping method to learn about it, and paid a lot of attention to my experience of the process. You can see the output of my research project here. Below is an overly long exploration of my experience researching and writing that blog post.

How I used to learn vs Knowledge Bootstrapping

My learning method has changed wildly over the years. When I was in undergrad, I thought that going to lectures was how you learned things and I barely ever studied anything aside from my own notes. This worked fine for undergrad, but didn’t really prepare me to do any on-the-job learning or to gain new skills. I spent an embarrassingly long time after undergrad just throwing myself really hard at problems until I cracked them open. If I was presented with a project at work that I didn’t immediately know how to do (and that a brief googling didn’t turn up solutions for), then I would just try everything I could think of until I figured something out. That usually worked eventually, but took a long time and involved a lot of dumb mistakes. And when it didn’t work I was left stuck and feeling like I was a failure as a person.

When I went back to college to get a Master’s degree, I knew I couldn’t keep doing that. I had visions of getting a PhD., so I thought I’d be doing original research for the next few years. I had to get good at learning stuff outside of lectures. My approach to this was to say: what did my undergrad professors always tell me to do? Read the textbooks.

So in grad school I got good at reading textbooks, and I always read them cover-to-cover. I didn’t really get good at reading papers, or talking to people about their research or approaches. Just reading textbooks. This was great for the first two years of grad school, which were mostly just taking more interesting classes. I did a few research projects and helped out in my lab quite a bit, but I don’t think I managed to contribute anything very new or novel via my own research. I ended up leaving after my Master’s for a variety of reasons, but I now wonder if going through with the PhD would have forced me learn a new research method.

Since grad school, my approach to learning new things, answering questions, and doing research has been a mix of all three methods I’ve used. I’ll read whatever textbooks seem applicable from cover to cover, I’ll throw myself at problems over and over until I manage to beat them into submission, and I’ll watch a lot of lectures on youtube. All of these methods have one thing in common: they take a lot of time. Now that I have a family, I just don’t have the time that I need to keep making the progress I want.

This is why I was so interested in AcesoUnderGlass’s research method. If it worked, it would make it so much easier to do the things I was already trying to do.

Knowledge Bootstrapping Method

My (current) understanding of her method is that you:

1. figure out what big question you want to answer
2. break that big question down into smaller questions, each of which feed into the answer to the big question
3. repeat step 2 until you get to concrete questions that you could feasibly answer through simple research
4. read books that would answer your concrete questions
5. synthesize what you learned from all the books into answers to each of your questions, working back up to your original big question

This is a very question-centered approach, which contrasts significantly with my past approaches. It seems obvious that breaking a problem down like this would be helpful, and honestly I do a lot of problem-reductionism during my beat-it-into-submission attempts. Is this all there is to her super-effective research method?

Elizabeth spends a lot of time on the right way to take notes, going so far as to show templates for how she does it. When I first saw this, I thought it would be useful but not critical. As I’ll discuss below, I now think some of the templating does a lot of heavy lifting in her method.

Furthermore, she based her system around Roam. I’ve been hearing an enormous amount about Roam over the past year or so. People in the rationality community seem enamoured of it. At this point it mostly seems like a web-based zettelkasten to me, and I already use Zettlr. Zettlr is also free, and stores data locally (my preference). It’s intended to be zettelkasten software, but I mostly just use it to journal in and I’m not very familiar with many of zettelkasten features of it. I decided to use that for my project, since it’s already where I write most of my non-work writings and it seems comparable to Roam.

Elizabeth shared several sample pages from her own Roam research. When I browsed Elizabeth’s roam it seemed super slow. I assume there’s something going on with loading up pages on somebody else’s account that makes it slower, as the responsiveness seemed unusable to me.

Ironically, zettlr crashed on me right after I posted my research results to my blog. I ended up having to uninstall it completely to install a new version in order to get it working again.

Questions

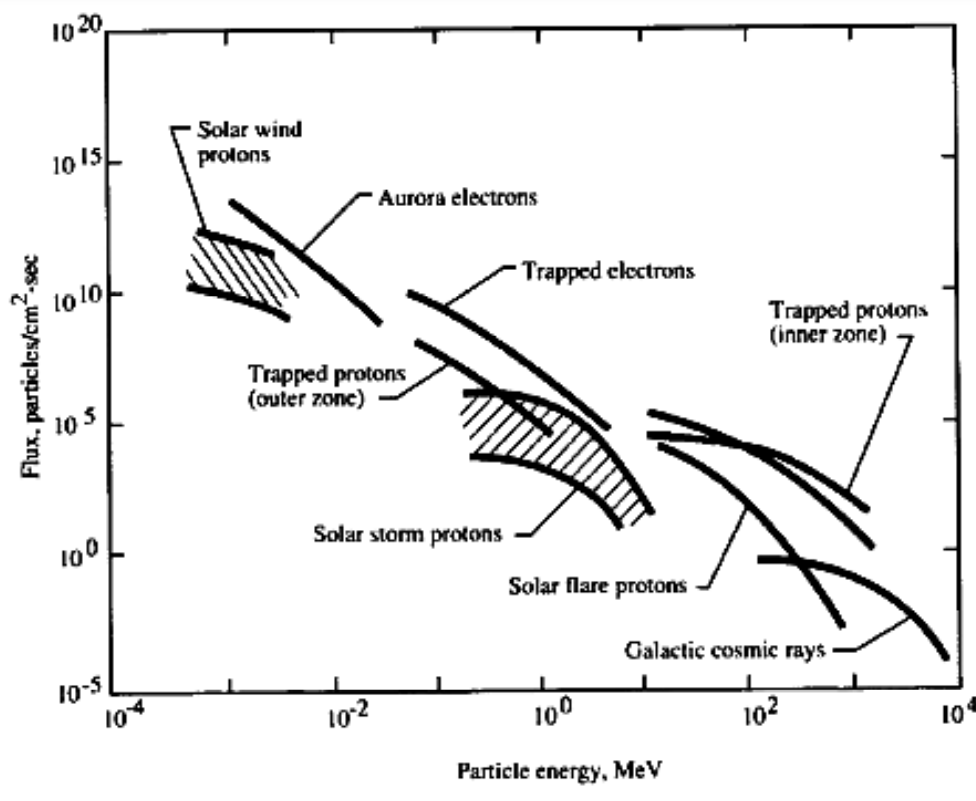
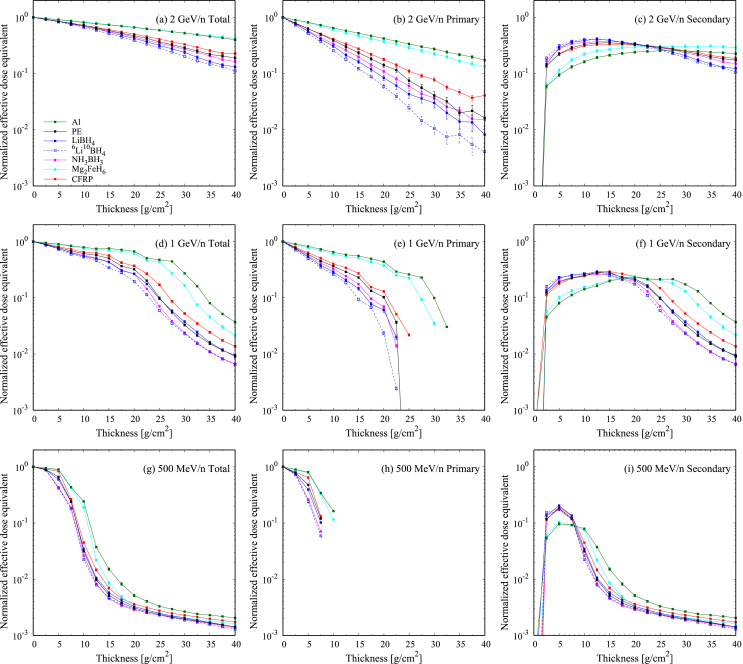
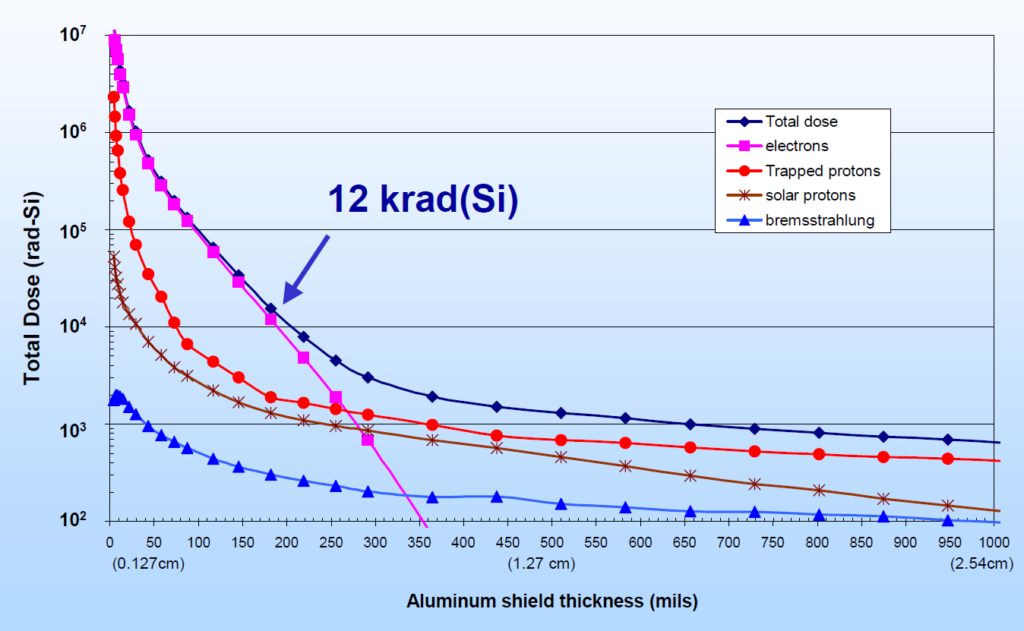
For my test project, I wanted to do a small investigation to see what Knowledge Bootstrapping was like. Elizabeth gives a couple of her own examples that involve answering pretty large and contentious questions. I picked something small just to get a sense for the method, and decided to learn how people protect electronics from radiation in space. I’m interested in this topic just as a curiosity, but it’s also useful to have a good understanding of it for my job (even though I’m mostly doing software in space these days).

I want to talk a bit about why that choice ended up being better than any alternative that past-me could have chosen.

The rationality and effective-altruism communities have infected me with save-the-world memes. People deeper in those communities than me seem to express those memes in different ways, but there’s definitely a common sense of needing to work on the biggest and most important problems.

This particular meme has been a net-negative for me so far. Over the past few years, I sometimes asked myself what I should do with my life, or what my next learning project should be, or what my five year plan should be. I approached those questions from a first principles mindset. I would basically say to myself “what is utopia? How do I get there? And how do I do that?” and try to backwards chain from this very vague thing that I didn’t really understand.

This never worked, and I’d always get stuck trying to sketch out how the space economy works in 2200 instead of chaining back to a question that’s useful to answer now. Because I was approaching this project with the mindset of “let’s experiment with something small to see how Elizabeth’s advice works”, I just took a question I was curious about and that would be useful to answer for work. That was amazingly helpful, and I now think that when choosing top level questions I should go with what I’m curious about and what feels useful, and just avoid trying to come up with any sort of “best” question.

The crucial thing here seems to be learning something that feels interesting and useful, instead of learning something that you feel like you should learn. I still think doing highly impactful things is important, but I’m left a bit confused about how to do that. The thing I’ve been doing to try to figure what’s most important has been sapping my energy and making me feel less interested in doing stuff, which is obviously counterproductive.

Question Decompositions

Decomposing my main question into sub-questions was a straightforward process. It took about five minutes to do, and those sub-questions ended up guiding a lot of my research and writing.

One failure mode that I have with reading books and papers is that it can be hard to mentally engage with them. This is one of the reasons that I have tended to read textbooks cover-to-cover. It makes it easier to engage with each section because I know how it relates to the overall content of the book. When I’ve tried reading only a chapter or section of a book, new notation and terminology has often frustrated me to the point of giving up or just deciding to read the whole thing.

Having the viewpoint of each of my sub-questions let me side-step that issue. For each paper, I could just quickly skim it to find the points that were relevant to my actual questions. Unknown notation and terminology became much easier to handle, because I knew I didn’t have to handle all of it. If something didn’t bear directly on one of my sub-questions (say because it dealt more with solar cycles than with IC interactions), I could safely skip it. If it was important, I knew I only had to read enough to understand the important parts, and that bounded task helped me to keep my motivation up.

When I finished reading some paper, it was always clear what my next step was. I just go back to my list of questions and see which ones are still not answered. Sometimes the answer to one would create a few new questions, which I would just add to my list.

This also explains why breaking the question down into parts at the beginning is more useful than the decomposition I do when I’m debugging something. By starting with a complete structure of what I think I don’t know, I have context to think about everything I read. That lets me pick up useful information quicker, because it’s more obvious that it’s useful. I’ve had numerous debugging experiences realizing that a blog post I read a week ago actually did contain an unnoticed solution to my problem. By starting with a question scaffold, I think I could speed that process up.

Sources

Elizabeth emphasizes the use of books to answer the questions you come up with. She spends at least one blog post just covering how to find good books. I suspect that this is a bigger problem for topics that are more contentious. The question that I was trying to answer is mostly about physics, and I didn’t have to worry too much about people trying to give me wrong information or sell me something.

I also didn’t particularly want to read 12 books to answer my question, so I decided at the beginning that I’d focus on papers instead. Those tend to be faster to read, and I thought they’d also be more useful (though if I could find the exact right book, it might have answered all my questions in one fell swoop).

I did have some trouble finding solid papers. Standard google searches often turned up press releases or educational materials that NASA made for 6th graders. Those didn’t have the level of detail I needed to really answer my low level questions.

So my method for finding sources was mainly to do scattershot google searches, and then google scholar searches. My search terms were refined the more I read, and I tweaked them depending on which specific sub-question I was trying to answer. When I found a good paper, I would sometimes look at the papers it cited (but honestly I did this less than might have been useful).

In general I think I learned the least from this aspect of the project. Part of this might be that my question just didn’t require as much information seeking expertise as some of the questions that Elizabeth was working on. Part of me wants to do another, slightly larger, Knowledge Bootstrapping experiment where I address a question that is less clear cut or more political.

One thing I did notice while I was doing the research was that a part of me sometimes didn’t want to look things up. It wanted to answer the questions I posed via first principles, and the idea of just looking up a table of data seemed like cheating. This reluctance may come from a self-image I have of someone who can figure things out. Looking things up may challenge that self-image, leading me to think less of myself. I think this is a pretty damaging strategy, though it may explain a bit of my old beat-it-into-submission method of solving technical problems. I think it might be useful to explicitly identify to myself if I’m trying to finish a project or to challenge myself. If I’m facing a challenge question, then working it through on my own is noble. If I’m trying to finish a project, then I’m just wasting time. I’d like to not have moral or shame associations in either case.

Reading and Notes

Reading and note-taking are definitely where the Knowledge Bootstrapping process really shines. Being able to efficiently pull information out of text can be difficult, and Elizabeth uses even more structure for this than I think she realizes (or at least more than Knowledge Bootstrapping makes explicit).

Her strategy for note-taking is:

1. make a new page for each source using a specific template
2. fill in a bunch of meta-data about the source
3. brain-dump everything you already think about the source
   • the explicit purpose for this is that it gets the thoughts out of your head, letting you actually focus on the source information
   • I suspect that a large part of the benefit is that you explicitly predict what the source will say, making it easier to notice when it says something different. That surprise is likely the key to new information
4. fill in the source’s outline (I never did this step)
5. fill in notes for each section

Elizabeth’s recommendation is that if you’re not sure what to write down in the notes, you should go back to your questions and break them down further. I can confirm that after I had all my questions broken out, it was very easy to figure out what was relevant. This also made it easier to skim the source and to skip sections. I knew at a quick glance whether a chapter or section was related to my main question and had no compunctions about skipping around.

This is a pretty big difference to how I normally read things. I tend to be a completionist when I read, and I definitely feel an aversion to skimming or skipping content normally. In the past, I’d feel the need to read an entire source document in order to say whether it was “good” or if I “liked it”. I had a sense that if I didn’t read every word, I couldn’t tell people that I’d read it. And if I couldn’t tell people that I’d read it I wouldn’t get status points for it or something. Maybe there’s something here about reading not for knowledge but for status and identity.

The knowledge that I was reading for a specific purpose was very freeing, and I felt much more flexible with what I could read or not read.

In any case, I felt comfortable reading the sources just to pick out information, and I felt comfortable with my ability to pick out whatever information was important. What I was less comfortable with was recording that information in a useful way.

This is the main place that I would have liked more information from Knowledge Bootstrapping. When I looked at Elizabeth’s Roam examples, I was blown away by the structure of her notes. It’s not just well organized at a section level, each individual paragraph is well-tagged with claim/synthesis/Implication annotations. She also carefully records page numbers from the book for everything. There are also a lot of searchable tags that link different books together.

I don’t use Roam, so the immediate un-intuitiveness is likely one of the reasons that I find this so impressive. The amount of effort that she puts into her notes is kind of staggering, and I find them much closer to literal art than my own stream-of-consciousness rambling.

The thing is, my own stream-of-consciousness, concise notes are driven by a desire for efficiency. I don’t particularly want to stop and write down page numbers every couple of pages of a book. I’m certain that she gets a lot of benefit from it in terms of being able to review things later, I’m just not sure it would be worth it for me.

This is where my inexperience with my own tools, zettlr and markdown, really hampered me. I’m pretty sure I could get zettlr to do most of what Roam was doing, and maybe even do it efficiently and speedily. To get there, I would have had to stop doing one research project and start another research project on just using zettlr.

I would love to watch Elizabeth take notes on a chapter in real time, to see more of what her actual workflow is like. How much effort does she really expend in those notes, and does it seem worth it to me? Would it seem worth it to me for a more ambitious project? I think watching that would also help me learn the method a lot better than reading about how she does notes, as it would be directly tied to a research project already.

Synthesis

Synthesizing notes into answers to questions was conceptually easy, but logistically I was limited by the same inexperience with my tools as I was when I was taking the notes themselves. Before I do another research project, I want to learn more about using Zettlr (or another tool if I choose to switch) to make citations and cross-post connections.

During this research project, I would often take notes on a source into two different posts at the same time. I’d be putting all my notes directly into the notes doc for that source, then I would switch to my questions doc and start adding some data there immediately.

I noticed while doing my research project that I at times wanted to construct an argument between a couple of sources. “X says x, Y says y, how do I use both these ideas to answer my question?” I found actually doing this to be annoying, and I ended up not really doing much of it in my notes or in my synthesis.

That type of conversation between sources is one of the great strengths of the erstwhile Slate Star Codex (as well as many other blogs I love), so I want to encourage it in my own writing. I don’t normally do that by default, so having it seem desirable here seems like a strength of the method. Before I do something like this again, I’d want to remove whatever barriers made me averse to doing that kind of synthesis.

This is the first time that I’ve appreciated the qualitative differences between different citation styles. Prior to this, when I would write a paper or report, I’d just throw a link or title into a references section while I was writing and clean it up later. I’d pick whatever citation style was called for by the journal/class that I’d be submitting the paper to. I treated citations (and citation style) like something that was getting in the way of writing a paper and figuring things out.

Taking notes (and later synthesizing them) from a question-centered perspective showed me why citations are useful beyond just crediting others. If I were comfortable with an easy to use citation style (AuthorYear?), i could refer to the sources that way in my notes and in my synthesis docs and more easily create the type of “X says, Y says” conversations between sources that I think are so useful.

That seems to be the root of my aversion to doing this type of source vs source conversation. I knew I was going to post a blog with my synthesis, and the idea of going back and fixing all the citations into a coherent style made me not want to do it in the first place.

Elizabeth recommends writing out the answers to your sub questions in the same doc as the questions themselves. Step 9 of her extended process description is just “Change title of page to Synthesis: My Conclusion” because your questions now all have answers. I found this advice to be very helpful. I would sometimes get tired of just reading and note taking, and feel like I should be done. Then I’d go write up the answers to my questions, and in doing so I’d come to a point that I couldn’t really explain yet. That would re-energize me, as suddenly there was an interesting question to address. The act of organizing all the things I’d read about helped me focus on why I was interested in the question in the first place as well as what I still didn’t understand. This aspect of the process, creating questions and then long-form answering them in my own words, seems to cause me to automatically do the Feynman Technique.

KB and me

I liked this experiment. I learned what I wanted to learn on an object level, and doing it felt more free and curiosity driven than a lot of my reading and learning. I think regardless of what I do for future learning projects, I’ll definitely do the question decomposition part of KB again. I’m not quite sure about using the note-taking structure of the method; I’ll need to experiment with it a bit more.

I do think that I’d want to know better how to use my tools before I do the next project like this. For this first project, I had the excitement of doing a new thing a new way to keep me doing the method. I think once the excitement of a new method wears off, the friction of notetaking could stop me from doing it if I didn’t get good at markdown and zettlr/Roam first.

Honestly, I think one of the greatest benefits to this project was the introspection of trying to figure out how well I was learning. If I hadn’t been paying attention to my own thoughts and motivations, this project could have produced similar understanding of my original question without really giving me any information about how I learn or what emotional blocks were contributing to poor learning methods. That’s not really a part of Knowledge Bootstrapping on it’s own, but maybe having a backburner process running in my mind asking how my learning is going would help me more than it would slow me down.