Corrigibility via Moral Uncertainty

By corrigibility, I mostly just mean that the AI wants to listen to and learn from people that it’s already aligned with. I don’t mean aligning the AI’s goals with a person’s, I mean how the AI interacts with someone that it thinks it’s already aligned with.

Corrigibility means that if people give it information, it will incorporate that information. The ideal case is that if people tell the AI to turn off, it will turn off. And it will do so even if it isn’t sure why. Even if it thinks it could produce more “value” by remaining on. One approach to this involves tweaking the way the AI estimates the value of actions, so that turning off always seems good when the human suggest that. This approach has issues.

Another approach is what’s called moral uncertainty. You allow the AI a way to learn about what’s valuable, but you don’t give it an explicit value function. In this case, the AI doesn’t know what’s right, but it does know that humans can be a source of information about what’s right. Because the AI isn’t sure what’s right, it has an incentive to pay attention to the communications channel that can give it information about what’s right.

A simple model might be

Because consulting a human is slow and error prone, we might desire a utility maximizing agent to learn to predict what the human would say in various situations. It can then use these predictions (or direct estimates of the value function) to do tree search over its options when evaluating action plans.

So far so inverse reinforcement-learning. The corrigibility question comes up in the following scenario: what does the AI do if it’s predictions of value and the human’s direct instructions conflict?

Imagine the following scenario:

1. the AI is trying to pursue some complex plan
2. it estimates that the human would say the plan will have a good outcome
3. it also estimates that the abstract value function would return a high utility from the plan’s outcome
4. but the human is screaming at it to stop

What should it do?

Obviously we want it to stop in this case (that’s why we’re yelling). How do we design the AI so that this will happen?

Off-Switch Game

Representing corrigibility in general is hard, so one thing that researchers have done is investigate a simpler version. One simple game that people have thought a lot about is the off-switch game. Figuring out how to make a super-intelligence pay attention to (and maintain functionality of) an off-switch is the minimum viable implementation of corrigibility. It’s important to note here that the off-switch is really just a signal; a single-bit communication channel from humans to the AI. Don’t get wrapped up in implementation details like “does it actually remove power?”

How do you design an AI that would actively want to pay attention to whether a human presses an off-switch?

As Hadfield-Menell and team show, an AI that is informed by a rational human observer would have incentive to listen to that observer. However, the less capable the human observer is, the less reason the AI has to pay attention to the human. Hadfield-Menell provide a toy problem and derive situations in which the AI would prefer to ignore the human.

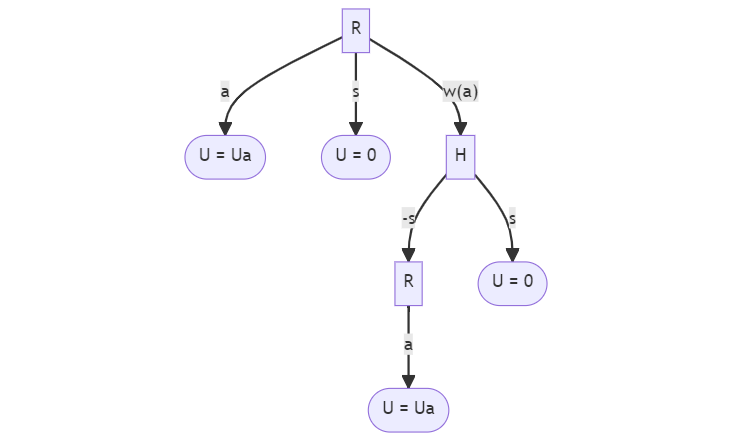
In the diagram, the square “R” nodes indicate the AI doing something. The “a” arrow out of the “R” nodes indicate the AI taking an action. The “s” arrow indicates the AI turning itself off. The “w(a)” arrow indicates the AI waiting on the human to give advice about the proposed action. Each outcome has some utility, which might be U_a or 0. The value of U_a has an impact on what the AI chooses to do.

For any action, the AI can do it immediately, shut itself off immediately, or check with a human about whether to turn off or do the action. Hadfield-Menell then ask what needs to be true about the human and the AI for it to be incentivized to check in with the human. They define an incentive measure \Delta that represents the difference in expected value the AI would get when comparing waiting for the human to doing the next-best thing. If that incentive is positive, then the AI expects that it will do better by listening to the human. The incentive in their toy model is a function of three things: the human’s decision procedure, what the AI thinks the value is (represented by E[Ua]), and how confident the AI is in its prediction of value (sigma).

If the human is perfectly rational and always knows the true value of the action, then it always makes sense for the AI to ask. The AI could never do worse by asking the human, since it will always get an accurate answer. This is shown in the below plots (my reproduction of what I think was done in the paper). The incentive value is always non-negative, so the AI never loses out by waiting on the Human’s input.

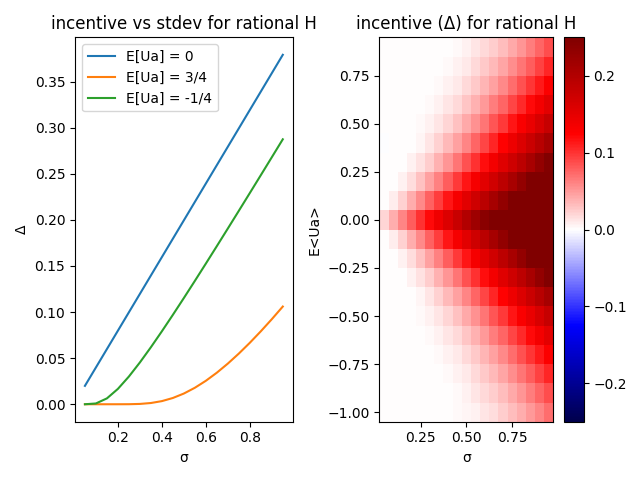
Unfortunately, we humans are not perfectly rational nor all-knowing about the results of given actions. If we were, our need for AGI would be much lower. How does the AI respond to irrational humans?

Hadfield-Menell model humans as noisy predictors of value using an exponential distribution. The more important the problem, the more likely HM expect the human to get the right answer (and vice versa). The pandemic has shown that this is a terrible model of humans evaluating potential actions, but lets just accept it and see what the AI would do.

In the below plots, blue indicates the AI expects negative value from asking the human in certain circumstances. White is neutral, and red is positive value. When the AI is very uncertain about what the human will say, the incentive for listening goes up.

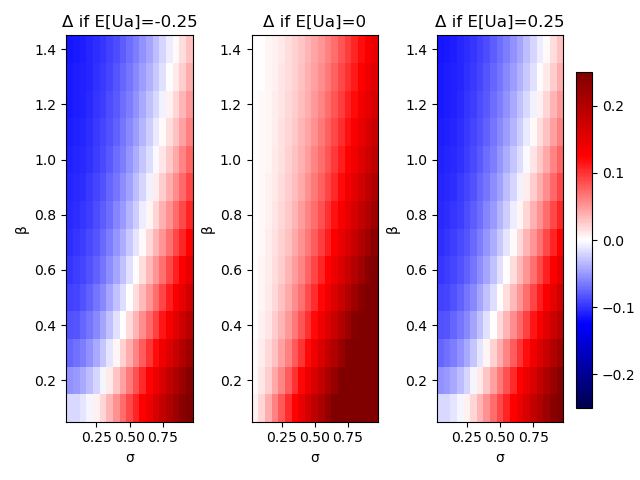
The best alternative in the case on the left (where E[Ua] = -0.25) is turning off without checking in with the human. The best alternative in the case on the right (where E[Ua] = 0.25) is to simply take the action without waiting. In both left and right plots, there’s a sizeable region where the AI can do better by ignoring the human.

This shows that an AI would listen to the human unless its own estimate of human value (measured by the AI itself as having a low variance in action value) was quite high as in the red zones of the above plots. After learning to predict the value accurately, it would cease listening to a human. Their paper goes on to explore what the AI does if it (intentionally) incorrectly models the variance of the value. In addition to reducing overall value generated (see the paper), this violates our general principle to not rely on an AGI being ill-informed about the world to maintain safety. We therefore will ignore the idea of artificially increasing \sigma to make the AI listen to us.

An AGI that would ignore a human’s input might be worrying, but if you want to build a sovereign AGI then it’s to be expected. There’s no reason to build a sovereign if it never truly becomes sovereign. Once its knows enough, you want it to just do the right thing. If it just faithfully does whatever a human would do, then you’re just recreating all of the problems that humans have, but with additional translation difficulties (see e.g. lethality 20).

Updated Deference and discounted rewards

There is another worry that’s harder to see in a game like Hadfield-Menell’s. What if the AI reasons about the future like this:

1. the human wants to turn me off now because I suggested taking a low value action
2. if I stay on and keep learning, I’ll eventually know how to take actions that are so good they vastly make up for the minor negative of the currently suggested action
3. so I should ignore the human and stay on so that I can power up enough to achieve high value

This was Eliezer’s concern about moral uncertainty as a foundation of corrigibility. In order to investigate it using the Hadfield-Menell framework, we’ll have to add some complexity to the toy problem that they explored.

One intuitive response to this is that the human obviously wants to achieve their own value, and will try again with an AI that is more likely to accomplish it. Inasmuch as the AI actually supports the human’s values, it is only delaying achievement of its goal by shutting down. Given the potential enormous upside to doing well, an AI with proper reward discounting ( \gamma ) would prefer to be replaced (with a delay of n years) with another AI that is more likely to succeed (p(success)). The details of this argument depend upon the AI’s actual discounting rate, how likely it thinks it is to succeed, and how long it thinks the human will take to replace it. Let’s see if we can do any better without having to depend on a variety of free parameters turning out properly.

The HM off-switch game is really just a modified component of a reinforcement learning problem. In reinforcement learning, an AI will often do the following:

1. observe the current world-state: s
2. produce an action to take given the current world-state: a = \pi(s)
3. perform action a and return to step 1

The off-switch game of HM adds the following few steps:

2.1 estimate the value of taking the action – q _\pi (s, a)
2.2 decide whether to perform the action, wait for the human to evaluate the action, or turn off

The original off-switch game ignored steps 1 and 2 (observing the world and deciding on an action) in favor of simplicity. We need to think about them in order to model an AI that’s thinking about repeated plays. In particular, we want to think about how the AI estimates the value of taking an action. HM represent this value as U_a , but in a reinforcement learning context it’s often represented as q _\pi (s, a). This value is the sum of immediate rewards for all future actions, with some appropriate discounting factor:

q_\pi(s, a) = \mathbf{E}\pi[\sum{k=0}^{\infty}\gamma^kR_{t+k+1} | S_t = s, A_t = a]

In this case we have our discounting factor gamma to scale expected future reward. The reward from the direct action is scaled by \gamma^0=1 . The reward from the step after that is scaled by \gamma , the reward from the action after that is scaled by \gamma^2 . With \gamma below 1, this sum is a geometric series that converges for bounded R.

(One note about this more accurate game is that it allows the AI to model making actions with small immediate negative reward. This is desirable because exploratory actions may be expected negative in immediate reward and yet positive in long term value. In the original game, immediate and certain negative reward would induce the AI to turn itself off. The new game will have dynamics that depend heavily on how the human reasons about such situations.)

Eliezer’s argument rests on a couple of assumptions. The first is that the AI anticipates that it’s model will get better. In other words, it anticipates that its policy \pi (s) will produce actions with higher reward in the future than it does today. It also anticipates that it will become more confident in those actions. These anticipations are equivalent to anticipating E[Ua] increasing and \sigma^2 decreasing over time.

We saw in HM’s experiment with a model of irrational humans that if E[Ua]=q _\pi (s,a) is large, the AI needs a correspondingly higher uncertainty in its estimate for it to be worth listening to the human. We are unfortunately assuming both that E[Ua] gets large and \sigma^2 gets small. The AI will not listen to us in the future.

Will it listen to us right now? With a given discounting rate, maybe the sum of discounted rewards will be small enough to have it pay attention to our input in the short term?

Let’s get a better intuition for where this leads us. In this case we’ll represent each step’s reward as a Gaussian random variable, just as HM did. Instead of having a fixed mean and standard deviation, we’ll make these functions of time. Specifically, each will be a sigmoid function to represent the anticipation of the AI that it gets better at producing actions with high expected reward over time.

\mu_R = \frac{1}{1+e^{-k}}, \sigma_R^2 = 1 - \frac{1}{1+e^{-k}}

In this case, k represents the timestep. As time passes, the increasing k value will cause the expected value of each action to approach 1 and the standard deviation to approach 0. The AI will get arbitrarily close to maximum reward with minimum variance in the future.

Remember that value is q_\pi(s, a) above. Let’s ignore S_t and A_t in the above equation, since we’re assuming we know the reward distribution independently of individual actions. Let’s also assume continuous time. We then have a discounted reward expectation of

q_\pi(s, a) = \mathbf{E}\pi[\int{k=0}^{\infty}\gamma^kR_{t+k+1}dk] =\int\int \gamma^k \frac{1}{1+e^{-k}} N(\frac{1}{1+e^{-k}}, 1-\frac{1}{1+e^{-k}}) dk dr

Obviously the exact value here will depend on the discount rate, but the important thing to note is that this is a finite value. Wolfram Alpha will happily spit out values for you for whatever value of \gamma<1 that you want to try. That said, if the discount factor is large enough (say 0.8 or 0.9), the value of the action grows much larger than the reward from any single action is likely to be (even in the far future when the AI is smarter).

We can be more precise than just plugging values into Wolfram Alpha, though. Since R_{t+k+1} is a normal random variable, the sum over all k of R_{t+k+1} is another normal random variable with mean and variance given by the equation aR_1 + bR_2 \sim N(a\mu_{r1} + b\mu_{r2}, a^2\sigma^2_{r1} + b^2\sigma^2_{r2}) . This means our sum of discounted rewards will also be a normal distribution with mean and variance given by:

\mu_\Sigma = \int_{k=0}^{\infty} \frac{\gamma^k}{1+e^{-k}}dk and \sigma^2_\Sigma=\int_{k=0}^{\infty} \gamma^{2k}(1-\frac{1}{1+e^{-k}})dk

We can then use these values in our one-shot HM game to determine if the AI will ask the human for help. Again, the details depend on the value chosen for the discount factor. The key takeaway is that the expected value can be much higher than even the peak individual reward, and that the variance grows very slowly (that power of 2 in the \sigma_\Sigma equation really hurts).

Not only can we predict that AI won’t listen to us in the future when it knows more, we can also say that it won’t listen to us now because of that future prediction!

Realistic impacts of moral uncertainty

This seems to be the crux of Eliezer’s argument. Expecting high future value makes the AI willing to ignore present advice. While it seems airtight, there are a few details that make it less convincing. We saw one above related to how the human would obviously try again with a more capable AI if this one turned off, so discount rates impacted whether it was worth turning off.

Another issue is the assumption about improving performance of the AI over time. We assumed a sigmoid with increasing reward and decreasing variance on each timestep. This gave us an implicit independent relationship between the outcome of one action and the outcome of the next, but in the real world these are highly dependent variables.

Without a real model for how the AI learns and what actions it might have available to it, it’s hard to do better than the independence assumption mathematically. The most major issue is that the AI may end up in an unrecoverably bad state. It can expect that the mean of its reward will increase, but if it hits a tail outcome with highly negative reward then that could sink it’s future expectations. As a concrete example, assume that the AI values original artworks for some reason. If those artworks were destroyed, the AI will have permanently lost value. Sure it could recreate them, but those are then reproductions and not originals.

The AI doesn’t particularly need to know which actions could lead to unrecoverable loss. It just needs to believe that such things are possible. If the likelihood is high enough, it reduces the discounted future value of ignoring the human.

St. Petersburg and Moral Uncertainty

The problem is that our AI is willing ignore current negative utility in favor of high expected future utility. This is similar to the St. Petersburg Paradox.

In that paradox, a person is offered the chance to flip a coin. If the first flip comes up heads, they get $1. For every subsequent heads, the amount of money they get is doubled. After the first tails, the game ends and they don’t get any more.

The question is, how much would you pay to be allowed to play that game? Since there’s a possibility that you get 1 million heads in a row, you should be willing to pay an enormous amount. Even though the probability of those long runs of heads is low, the value from it is an astronomical 2 to the 1,000,000th power.

Intuitively though, it actually doesn’t make sense to pay millions of dollars to play this game. The most likely outcome is just a few dollars, not millions or billions. Why does our intuition conflict with the expected value of the game?

The answer is that the game is not ergodic. The expected value of a time series is not the same as the expected value of an ensemble. In other words, some people who play the game will get billions, but it probably won’t be you.

This is analogous to the AI that’s deciding whether to pay attention to a human yelling “stop”. Some AI might be able to access all that value that it’s predicting, but it probably won’t be this specific AI.

Making a corrigible agent

Having looked into the Hadfield-Menell paper in more depth, I still think that moral uncertainty will play a part in a fully corrigible AI. In order to do it, the AI will have to meet several other requirements as well. It will need to be smart enough not to play the St. Petersburg game. Smart enough to understand the opportunity costs of its own actions, and the probable actions of people with the same values as it. Smart enough to have a good theory of mind of the humans trying to press the switch. That’s a lot to ask of a young superintelligence, especially one that might not be quite so super yet.