This problem comes from Chapter 4 of An Introduction to Decision Theory.
Suppose I show you two envelopes. I tell you that they both have money in them. One has twice as much as the other. You can choose one and keep it.
Obviously you want the one that has more money. Knowing only what I’ve told you already, both envelopes seem equally good to you.
Let’s say you choose the left envelope. I give it to you, but before you can open it I stop you and tell you this:
You’ve chosen one envelope. Do you want to open this one or switch to the other one?
You think about this, and come up with the following argument:
I chose the left envelope, so let’s assume it has L dollars in it. I know that the other envelope has L/2 dollars with 50% probability and 2L dollars with 50% probability. That makes the expected value of switching envelopes 1/2(L/2) + 1/2(2L), or 5/4 * L. So it does make sense for you to switch to the right envelope.
The decision matrix for this might look something like:
| R = L/2 | R = 2L | |
|---|---|---|
| Keep L | L | L |
| Switch R | L/2 | 2L |
But just as you go to open the right envelope, I ask you if you want to switch to the left. By the same argument you just made, the value of the left envelope is either R/2 or 2R and it does make sense to switch.
Every time you’re just about to open an envelope, you convince yourself to switch. Back and forth forever.
The Real Answer
Obviously the original reasoning doesn’t make sense, but teasing out why is tricky. In order to understand why it doesn’t make sense to switch, we need to think a bit more about how the problem is set up.
Here’s what we know:
- L is the value of money in the left envelope
- R is the value of money in the right envelope
- R + L = V, a constant value that never changes after you’re presented with the envelopes
- L = 2R or L = R/2
There are actually two ways that I could have set up the envelopes before offering them to you.
Problem setup 1:
- choose the value in the left envelope
- flip a coin
- if tails, the right envelope will have half the value of the left
- if heads, the right envelope will have twice the value
Problem setup 2:
- choose the total value of both envelopes
- flip a coin
- if tails, the left envelope has 1/3 of the total value
- if heads, the left envelope has 2/3 of the total value
Both these formulations result in the same presentation of the problem, but they need different analysis to understand.
Problem Setup 1: L = 20
Let’s make things concrete to make it easier to follow. In problem setup one we start by choosing the value in the left envelope, so let’s set it to $20. Now the game tree for the problem looks like this:
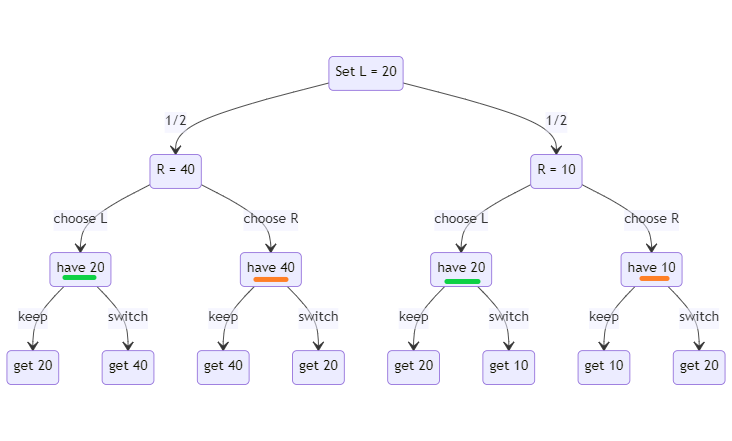
We’re showing the true game state here, but when you actually choose the Left envelope you don’t know what world you’re in. That means that, once you choose the left envelope, you could be in either of the “have 20” states shown in the game tree (marked in green). Let’s look at the decision matrix:
| R = L/2 | R = 2L | |
|---|---|---|
| Keep L | 20 | 20 |
| Switch R | 10 | 40 |
In this case, the outcomes are which one of the two green-marked worlds you’re actually in. At the time you’re making this choice, you don’t know what L is. We’re filling in numbers from the “god-perspective” here.
Now the math here matches what we saw at first. The benefit of switching is 10/2 + 40/2 = 25. The benefit of staying is 20. So we should switch.
Once you switch, you’re offered the same option. But in this case the decision matrix looks different. You don’t know which of the orange-marked R states you’re in, but they’re both different values:
| L = R/2 | L = 2R | |
|---|---|---|
| Keep R | 40 | 10 |
| Switch L | 20 | 20 |
Now it makes sense to keep R! The reason is that the “R” value is different depending on which world you’re in. That wasn’t true of L because of how the envelopes were filled originally.
With this problem setup, it makes sense to switch the first time. It doesn’t make sense to switch after that. There’s no infinite switching, and no paradox.
In fact, it only makes sense to switch the first time because we “know” that the Left envelope has a fixed amount of money in it (the $20 we started the problem with).
If instead we didn’t know if the fixed amount was in the left or the right, we would be equally happy keeping or switching. That’s because both options would give us a 50/50 shot at 5/4 the fixed value or the fixed value.
Problem Setup 2: V = 60
In the second setup, the questioner choose the total value of both envelopes instead of choosing how much is in one envelope. Let’s set the total value to be $60. That means that one envelope will have $20 and the other will have $40, but we don’t know which is which.
The game tree for this problem is different than the last one:
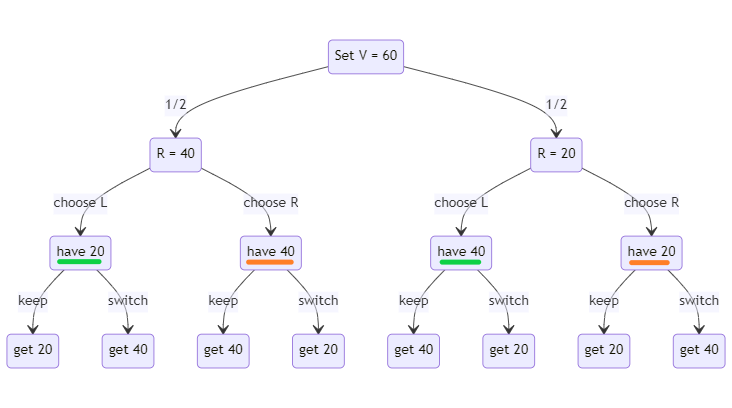
Now assume that I choose the Left envelope, just like before. In this case I don’t know which of the two possible worlds I’m in. So I don’t know if I have $20 or $40. This makes the decision matrix look like this:
| R = L/2 | R = 2L | |
|---|---|---|
| Keep L | 40 | 20 |
| Switch R | 20 | 40 |
In this case it’s very clear that the situation is symmetric from the start. The “L value” is different depending on whether you’re in the “R = L/2” or “R = 2L” world. There’s no reason to switch even once.
The fundamental mistake
The fundamental mistake that originally led to the idea of a paradox is this: we assumed that the amount of money in the left envelope that you chose was fixed.
It is true that once you choose an envelope, there’s a certain unchanging amount of money in it.
It’s also true that the other, unchosen, envelope either has twice or half the amount of money in it.
It is not true that the amount of money in your envelope is the same regardless of whether the other envelope has double or half the amount. You just don’t know which world you’re in (or which branch of the game tree). The expected value calculation we did at first used a fixed value for what was in your current envelope. The key is that if you’re making assumptions about what could be in the other envelope, then you need to update your assumption for what’s in your current envelope to match.